Eldarica-P

Reachability Checker for Unbounded Petri nets

Eldarica-P is a CEGAR-based reachability checker for Petri nets. Eldarica-P was developed in the context of a visit to LaBRI in Bordeaux in 2013, and in collaboration with Jerome Leroux. Since Eldarica-P works in a fully symbolic way, it can handle bounded as well as unbounded Petri nets; in the latter case, the number of tokens in a Petri net is not bounded, and the number of reachable configurations is therefore infinite. In addition, Eldarica-P can be applied to Petri nets whose reachability set is not definable in Presburger arithmetic.

The checker is entirely written in Scala, and based on two other systems:

Download and Start

We only provide a binary version of Eldarica-P at the moment. Please contact me if you are interested in working with the source code. Also, I am always interested in hearing about experiences with the tool (positive and negative)!

After downloading the jar-file of Eldarica-P, you should be able to run the model checker using any standard Java virtual machine: 

> java -jar eldarica-p-20140129.jar
Reading Petri net from stdin ...
A list of the available options can be obtained via -h: 
> java -jar eldarica-p.jar -h
Eldarica-P - The Unbounded Petri Analyser
(Build 2014-01-29)
(c) Philipp Rümmer, 2014

Based on:
Eldarica, http://lara.epfl.ch/w/eldarica
Princess, http://www.philipp.ruemmer.org/princess.shtml

General use:
  java -jar eldarica-p.jar <options> <filename.net>

If no filename is specified, inputs are read from stdin.

Options:
 -interpolationAbstractions=<options>
     where <options> is a comma-separate list of
       globalOrthogonalSpace
       accelerateSingleActions
       accelerateIncreasingCycles
     default: all
 -controlGroups=<number>
     maximum number of control groups to handle explicitly
     default: 2

First Steps

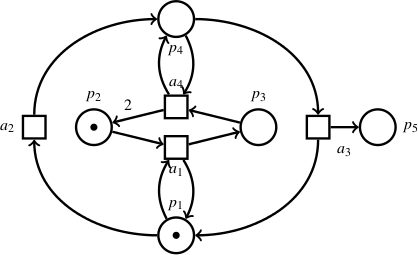
As a first example, you can put the following Petri net definition (left box) into a file simple.net: 

net {"Exponential reachability set"}

tr t1 [] p1 p2 -> p1 p3
tr t2 [] p1 -> p4
tr t3 [] p4 -> p1 p5
tr t4 [] p4 p3 -> p2 p2 p4

pl p2 (1)
pl p1 (1)

final p2 (5)
final p5 (1)
Petri net

The lines starting with tr define transitions; lines starting with pl specify the initial number of tokens in a place (any place not mentioned is assumed to be empty); lines starting with final specify the configuration whose reachability is to be checked (places not mentioned may hold any number of tokens). In the example, Eldarica-P will check whether any configuration is reachable in which p2 contains 5 tokens and p5 contains 1 token.

Running Eldarica-P on this example will give you something like: 

> java -jar eldarica-p.jar simple.net
Reading Petri net from simple.net ... 
5 places, 4 transitions

Computing control groups ...

[...]

UNREACHABLE

Inductive invariant:
p1 + p4 = 1 & (p1 = 0 | (p2 = 0 & p5 = 0 & 1 >= p3 & p3 >= 0) | [...]

There is a second, more flexible way to specify final configurations. This is done using the keyword finalConfiguration, followed by a Presburger formula defining the considered configurations: 

tr t1 [] p1 p2 -> p1 p3
tr t2 [] p1 -> p4
tr t3 [] p4 -> p1 p5
tr t4 [] p4 p3 -> p2 p2 p4

pl p2 (1)
pl p1 (1)

finalConfiguration (p2 = p3 & p5 > p2)

Documentation

The techniques implemented in Eldarica-P are described in section 9 of the following article:

Further Examples

We provide a small collection of benchmarks from the literature.